Creating a decent Netflix password

Pop quiz you’re at an Airbnb in Montauk with 10 friends. After a rousing game of flip cup, the party is threatening to slow down… until someone says they want to watch the new Beyoncé live concert film. Someone else navigates to the Netflix icon on the AppleTV. But then… bam! Log in to Netflix? You want to help. You want to offer your log in, confident that in a few days you’ll remember to “LOG OUT OF ALL DEVICES” so that the next guests at this Airbnb don’t watch ahead of you in Peaky Blinders. But then you remember that your Excellent password, stored in your password manager that you have access to on your phone, looks something like “qmYY3Pw7[~y” or “$O/\S/I;~9q”. How long will it take you to read or type out that string of characters on AppleTV’s linear keyboard?

We can do better. We want a password that is both convenient to enter in the situation above, but also still relatively secure.

I’ll walk us through a series of claims, using almost everything I’ve learned about passwords over the past few years, toward a process for creating a decent password for the situation described above.

Use words

First, we’re going to use words rather than random characters.

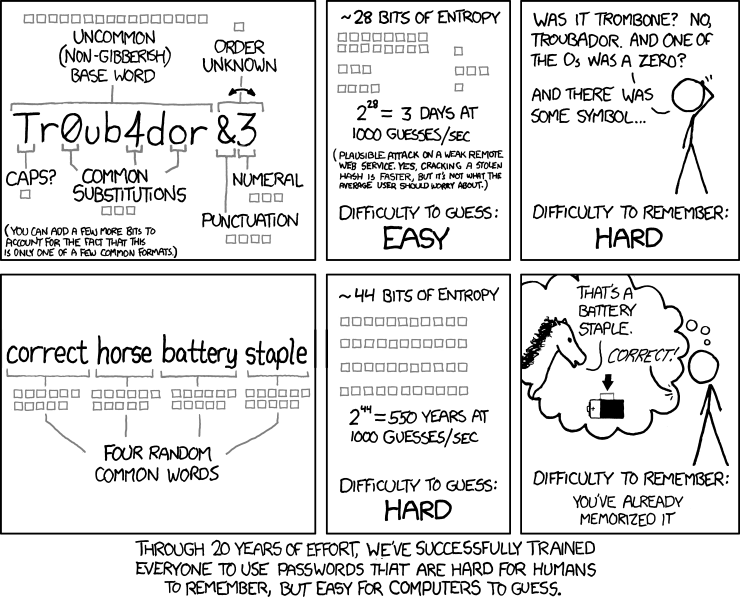
correct horse battery staple

If you’re reading your password to someone inputting it into a device, it’s much quicker to read 4 to 6 words than 15 to 25 characters. It’s also more error resistant. If your friend hears “correcb” they can probably turn that into “correct”. And if you’re typing the password in yourself, while using words is more characters, it’s easier to “carry” a word in your head mentally as you move from the password manager app on your phone to the TV.

Plus, it’s usually a pain to switch to the numbers/punctuation keyboard on smart TVs, and it costs “clicks” (more on this below).

So we could select, say, 4 random words and make that our password – like carving exceeding boned legislate. But we can be a bit smarter about this…

Fewer button presses?

What list of words should we use to create our Netflix password? A classic choice is the EFF long list. This list has 7,776 words on it, so each word in your passphrase gives 12.925 bits of entropy.

(Some security assumptions: Going forward, we will assume that our attacker has the exact word list that we used to create our passphrase. Below, I’m going to assume that 51 bits of entropy is sufficient for Netflix, but users can increase that based on their threat model by either using more than 4 words from the final list, or by creating a longer list themselves.)

But what if we made a list that is more optimized for our Montauk party? We’re trying to minimize the number of “clicks” we or a friend has to make on the remote as party enthusiasm wanes. What if we assume the linear keyboard that AppleTV uses. It looks like this:

abcdefghijklmnopqrstuvwxyz

Then, we could “score” a given word by how many “clicks” it takes to type, including the left-right movement between characters. So for example, “bad” would score 6 clicks. “zap” would cost 43 clicks.

First, let’s find a large list of common English words to start from. How about we scrape Google Books for frequently used words since 1975. Let’s arbitrarily take the 18,000 most common words that are 3 letters or longer.

We could then sort these 18,000 words by click score (given our assumed linear keyboard), listing low click scores first. Then we could take the top 7,776 words from this list and randomly select, say, 4 words to make a decent Netflix password like “rust gps fearing scaled” or “vat tamil sly sadly”.

Not bad! But what about those spaces between the words? Those cost clicks too! Do we need them? Can’t we just mash the words together?

Uniquely decodable lists

If we were to remove the spaces from these passphrases (“rustgpsfearingscaled”) (i.e. remove the delimiter), we would save a bunch of clicks (navigating to and from the “space” button), but we would also expose ourselves to a subtle security issue. Can you spot it?

As a brief example, if a list has “boy”, “hood”, and “boyhood” on it, users who specified they wanted two words worth of randomness (entropy) might end up with “boyhood”, which an attacker guessing single words would try before moving on to two-word combinations. This is bad! We’re picking 2 (or 4) words based on important security assumptions, namely that an attacker, even one who has our exact word list, would have to work through 7776² possible combinations (or, if we’re using 4 words, 7776⁴).

Thankfully, we can protect ourselves from this issue by removing certain words from the list. In this toy example, if we removed the word “boy” from our list, we’d be safe to mash the words together without a delimiter. This is because “boy” is the only “prefix word” on the list - -the only word that is a prefix of another word on the list (“boyhood”).

Removing all prefix words (in this case, just “boy”) makes the remaining list something called a prefix code, a key concept in coding theory. Lists that are free of prefix words are guaranteed to be uniquely decodable. This is the property we’re interested in – this is what makes it safe to combine words without a delimiter, since they can be “decoded” in only one (unique) way. (This is how the EFF word lists were made safe to combine.)

Cool. We could remove all prefix words from our list and go with that (an example passphrase from such a list: “exotic officials flavors months” which we could safely make “exoticofficialsflavorsmonths”). But! As you might guess, removing all prefix words removes some great, quick-and-easy-to-type words (like “boy”)….

A new way to create a uniquely decodable word list, cutting fewer words

Ideally, we’d want to make our word list uniquely decodable while removing the fewest number of words possible. To see why, let’s dig into the procedure I’m using to create a uniquely decodable word list.

Let’s recap. We want our list to be uniquely decodable so that users can forgo using a delimiter between words. We’ve got a nice list of 18,000 words from Google Books, which is sorted by click costs. Ideally, our finished list would draw from the top of the list, since those cost fewer click. (More generally, we can say it is sorted by what we might call “desireability”.) But the list is not uniquely decodable.

As established above, one way to make a given word list uniquely decodable is to remove words. One method for removal is remove all prefix words. Let’s try that.

If we remove all prefix words from the 18,000 list, we get a list of 13,037. This is usable, but if we only need 7,776 words on our final list (making it the same length as the EFF long list – the number is a result of common dice having 6 sides), we can take fewer words from the 18,000 list. We’ll take words from the top of the sorted list, since we know those words have the lowest click scores.

It turns out that when we take the first 10,802 words from the list and remove prefix words, we get a 7,776 list. That’s neat! But can we do better? What if we could make a uniquely decodable, 7,776-word list using, say, only the first 10,000 words on the list? That resulting would list would be superior, since it couldn’t possibly have those 802 “worst” words from the original list.

Schlinkert pruning

Is there another way to make a list uniquely decodable, besides removing all prefix words? Well, turns out we could remove all suffix words (“hood”, in the above example). With English words at least, removing all suffix words seems to “save” more words than removing all prefix words, so that’s good. If we perform the test described above, but remove all suffix words rather than all prefix words, we only need to take the first 8,996 words. An improvement!

But is there an even better algorithm?

To learn more about this, I read about the Sardinas–Patterson algorithm. From Wikipedia:

In coding theory, the Sardinas–Patterson algorithm is a classical algorithm for determining in polynomial time whether a given variable-length code is uniquely decodable, named after August Albert Sardinas and George W. Patterson, who published it in 1953. The algorithm carries out a systematic search for a string which admits two different decompositions into codewords. As Knuth reports, the algorithm was rediscovered about ten years later in 1963 by Floyd, despite the fact that it was at the time already well known in coding theory.

Sardinas-Patterson only tells us whether a given list (or “code”) is uniquely decodable – basically a “yes, it’s uniquely decodable” or “nope, it’s not”. That’s neat, but what we really want an algorithm that takes a list and spits out a list of words to remove to make it uniquely decodable (and hopefully the list of necessary removals is short!).

To accomplish this, I tweaked the Sardinas-Patterson algorithm to create a new process that I call “Schlinkert pruning”. In rather rudimentary tests, Schlinkert pruning does remove fewer words than removing all prefix words or all suffix words. Awesome!

So, instead of removing all prefix words or all suffix words, we’ll “Schlinkert prune” our word list to (finally) get a safe list of low-click-cost words that we can safely combine and use.

If we “Schlinkert prune” the list, we only need to take the first 8,944 words. Admittedly that’s not much better than removing all suffix words (which required the first 8,996 words), but it is better! That’s our fewest words used yet! (I don’t know of any other algorithms to test, other than making all the words the same length, which would remove a lot of words.)

Final list

We’ve got our procedure down. I built it into my word list manipulation tool, Tidy, so you can actually do it yourself by taking the raw list and running tidy -AAAA --whittle-to 7776 -K -lL -o my_list.txt lists/raw/alpha-line.txt.

The resulting list is uniquely decodable and 7,776-words long, just as we wanted.

But in order to make a usable list, I wanted to make some cuts of my own. I decided to cut profane words, British spellings of English words, and Roman numerals. To remove some proper nouns, I also (somewhat controversially) only let through words found in the Linux list of English words found at /usr/share/dict/words. With all these additional cuts, I needed to take the first 11,047 words from the list of 18,000 to Schlinkert prune down to 7,776, but I think it’s worth it. (I’ll note here that, with these additional cuts, Schlinkert pruning was still the best method of the three!)

Finally, we now have a usable word list for our particular use-case: It’s made up of relatively common words, it’s uniquely decodable (and thus words can be safely combined), and it should be generally easy to input using our linear keyboard (thanks to us prioritizing words with low click scores).

Some example 4-word passphrases from this final list that we could use for Netflix and keep that Montauk party going:

areasfitnesscutsspotted
folderflungsmilesgrooves
savebuddolphinscouncils
hinderedpurpleslickchoose 
clotheddaisymotionlessoffense 

Obviously, don’t use any of the passphrases published in this blog post!

How to make your own passphrase, securely

One way to securely create a passphrase is to use physical dice, where a roll of 5 6-sided dice corresponds to one word from the long lists. Here’s my usable word list with corresponding dice rolls for you to use. If you use one of the short lists, you just need 4 6-sided dice.

If you want more than 51 bits of entropy, you can use more than 4 words from one of the long lists (more than 5 from one of the short lists – see below). Please use your own threat model!

To those who work on password generation software (either built-in to an online service sign-up flow or a password manager), I encourage you to imagine possibilities of using word lists tailored to users’ contextual needs.

What about other smart TV keyboard layouts?

Above, we assumed a Montauk house that had an smart TV with a particular linear keyboard.

Following the process above, we can make separate lists for other layouts. As you might expect, this results in different word lists. See this repo for more.

Short lists

I’ve also used this process to create shorter, 1,296-word versions of these lists. This number of words corresponds to rolls of 4 dice.

Each word from these lists adds about 10 bits of entropy to a passphrase, so you’d need to use 5 words from these shorter lists to get the same security as 4 words from the long lists. What makes the short lists appealing is that the words cost fewer clicks. Here are some sample passphrases from the short alpha-line list, each of which has 62 bits of entropy:

gloom propped sit cup tub fir
ache prone sly tied fled tip
four glad hog define boon cast
also tug abide skins lupus hike
cuts boron outputs utmost leg bet